Absement

Sometimes our minds light up with a private question just before we notice that same question flashing across all society. The experience might make us wonder if curiosity is an unseen wave force, something like a societal consciousness.

A recent reflection on the biographies of Isaac Newton, and Gottfried Leibnitz, and their simultaneous invention of calculus, produced a question I'd never before considered.

The Calculus Wars

Let's simplify this discussion with a universally understood prop, the automobile. As we drive, we go faster and slower, and ultimately stop someplace. That is we accelerate (by pushing the accelerator), drive at a preferred speed (velocity), and eventually decelerate with the brakes and stop.

At any particular time during the drive, we are at a particular spot on the road, going some particular speed, either speeding up or not. In the language of calculus we have a displacement from our starting point (a position), a velocity, and an acceleration.

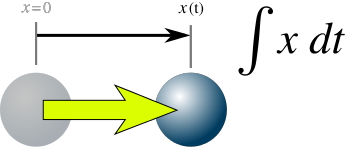
We can think of displacement as a history of the position of our car, train, space ship, or planet. In math lingo that's a function correlating time to position. The first derivative or our displacement function is the rate at which the location changes, called velocity, and the second derivative is the rate at which velocity changes, called acceleration. The third derivative, the rate at which acceleration changes, is conventionally called “jerk.” The fourth derivative is called “jounce” (sometimes "snap") and the fifth derivative is called "crackle." Beyond that are several other whimsical titles. We're right now just considering the position, the velocity and acceleration.

The other half of calculus, the integral, can be considered the anti-derivative or the inverse of the derivative, reversing its mathematical outcome, the way subtraction reverses addition, and division reverses multiplication. Take the integral of something and you get the function whose derivative produced it. Take the integral of acceleration and you get velocity, of velocity and you get displacement (position). When you take the integral of the displacement function you get something whose rate of change should be the displacement. But, what does that mean? What is its physical significance of the integral of displacement? I was stumped.

Now we get to the stimulus for my original question about curiosity. A search of on-line resources found several people who had recently, circa 2016, been asking about the integral of displacement. During the first decade of this century, that question was taken up by Dr. Steve Mann of the University of Toronto. He and a colleague invented a name, absement, for the time integral of displacement. Absement is a combination of two words, absence and displacement, for reasons that can best be grasped by reading some of Dr. Mann’s own work, but the point here is, there was no prior name for it, because no one had thought the question important enough to name.

You can get a feeling for the discussions about absement by perusing various web authors. Dr. Mann himself has invented a musical instrument based on use of the absement property in a fluid flow system. Click the title block to hear Dr. Mann playing his hydraulophone. One of his students has won a science contest by demonstrating, or measuring, the property of absement. It is a 21st century term. Your spell checker has probably caught up by now. Wiktionary discovered it some time after 2016, although Wikipedia has been on board for over a decade.

Surprisingly, I turned up no references to anyone who had been asking about the nature of the displacement integral prior to Dr. Mann. I expected to get a clutter of academic, and text-book references dating back centuries, thanks to the Google digitization project. We can read the nineteenth century musings of Riemann on his Zeta function, but nothing about the displacement integral prior to this century. Many of the current references express puzzlement, many are dismissive, saying there is not likely to be any use for the idea, while a few, like Dr. Mann and his colleagues, find exciting innovation buried in the concept.

The current popular wisdom about absement is everywhere, and condenses around the following idea. Absement is useful for measuring the net/average displacement, as you would divide this integral by the total time interval. It would also be useful for systems in which accumulated distance is dependent on a displacement and the length of a time of a given displacement. Examples include systems which expel power as a function of displacement, i.e. any kind of valve opening.

My lingering question is, what made this exploration of the integral of displacement pop into the collective consciousness over the last decade and a half. We’ve been doing calculus for centuries, and I’ve been doing it for decades. I don’t remember ever thinking about the integral of displacement before. Were there a few people in prior ages wondering about it, but unable to collaborate until the Internet came along? Or, did something propel this obvious question forward at this moment?

For me, the question just appeared, leaving me wondering why I’d never wondered about it before. I found other people similarly puzzled about why they’d never considered it before. Some of them were fascinated enough to invent language, write poetry, inspire students, create new inventions, develop new theories, and even hint at arcane explorations. One of the characters in a story I’m writing has a theory about all this, but I can’t get into that yet, except to say he is controversial. I’m hoping he will consent to explain it to me.

More recently, circa 2024, I thought ChatGPT could help. Our interaction is linked from a nearby picture, and as you can see, ChatGPT has already replaced Dr. Mann as originator of the word "absement." I've alerted Dr. Mann. I thought he should know.